
Last time, I showed you how Linear Algebra is the language machine learning models speak.
But how do those models actually learn from the data?
That’s where calculus comes in, like a genius superhero to save the day.
Calculus is like the brain of the model that tells it what to do…primarily, how to find the best answer!
It is like a navigation system for your machine learning models, whether predicting the right numbers, categorizing the right pictures, or trying to successfully deliver a sarcastic comeback to your in-laws.

🤔 What Is Calculus
In Machine Learning, think of calculus as the GPS towards the right answer.
Calculus is essential because it allows the machine learning model to learn from its mistakes and improve itself.
Which is kind of the whole point of machine learning.
Calculus is a branch of mathematics that studies continuous change. It provides the tools to measure rates of change (derivatives) and the accumulation of quantities (integrals).
Calculus is fundamentally divided into two main areas:
Differential Calculus: how fast something is changing.
Integral Calculus: the total amount of something that has changed.
In machine learning, differential calculus is the star of the show. It figures out how much a model's error (the difference between what the model predicted and the actual, correct answer) changes when you adjust its internal parameters.
This leads us to the superhero algorithm of machine learning: Gradient Descent (yes, the inspiration for my newsletter name is more than just a name. What a surprise.).

🧠 Gradient Descent
Imagine you’re blindfolded and dropped on the side of a mountain. Your only goal: find the lowest point in the valley. But since you can’t see anything, how do you move?
You shuffle one step at a time in the direction where the ground feels like it’s sloping downward.
Congratulations, you’ve just performed gradient descent.

Performing Gradient Descent or navigating adulthood? You decide.
Gradient Descent is the single most important concept that takes a model from "randomly guessing" to "making smart predictions."
How It Works
Remember this familiar-looking equation from middle school?
y = mx + b
It's the formula for finding the slope of a line (but of course, you already knew that 😉).
Well, gradient descent is basically the souped-up, super smart version of that.
Think of a model’s performance as a value we want to minimize (known as the error I mentioned above). The goal of gradient descent is to find the specific set of parameters that makes the value as tiny as possible.
It works by:
Starting with a guess.
Using calculus to find the direction that reduces the error the fastest.
Taking a small step in that direction. This process repeats over and over until the model's error is minimized and it has found the best possible answer.
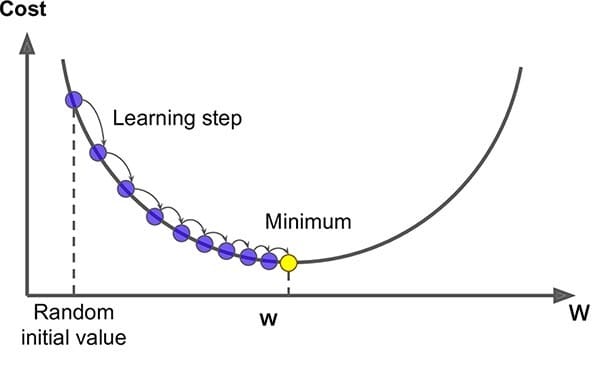
Image Credit: Saugat Bhattarai
Notice how the distance between the purple dots gets smaller as it approaches the minimum? This is because it helps the model get to the optimal solution (yellow dot) without shooting past it.
In other words, your model’s really trying NOT to let you down.

📏 Derivatives / Partial Derivatives
Now that we know gradient descent is the engine that guides your model, where does the engine get its instructions from?
That’s where derivatives and partial derivatives come in.
⏲ Derivative: Your Model’s Speedometer
At its core, a derivative is simply a measure of how fast something is changing at an exact moment.
It is like your model's speedometer. It's the math that tells a model how fast its error is changing at any given moment, like how fast your speed is changing on a road.
This is how the model knows if tweaking a parameter is making things better or worse, and by how much.
📝 Partial Derivative: Recipe For Success
A partial derivative measures the effect of changing just one variable on a function, while keeping all the others the same.
Imagine you're trying to figure out how much the flavor of a soup changes as you add more salt, but you want to ignore the effect of the pepper or basil at that exact moment. The partial derivative tells you the precise effect of only the salt.
In machine learning, this is essential because a model's error is based on hundreds or thousands of different parameters (variables). A partial derivative lets the model figure out how much to adjust each parameter to reduce the overall error.

🔗 The Chain Rule
The Chain Rule is a formula that basically says:
“If A affects B and B affects C, then A secretly affects C too, and you figure it out by multiplying the links.”
Imagine tacos make you happy. Then let’s say happiness makes you more productive — so basically tacos affect your productivity, but you measure it by multiplying those two effects.
In machine learning, this is gold.
A neural network is basically tacos stacked on tacos (functions inside functions). The chain rule helps us trace back a tiny change in weight that affects the final error, which is exactly what we need to know to update the model.

🌟 Conclusion
And that’s a wrap on why calculus is the engine of machine learning!
Keep in mind, we’ve only scratched the surface of this complex monster.
There’s so much more to calculus that I look forward to showing you to prove that it isn’t just a headache from a college exam.
Next up, we'll tackle the world of probability and statistics, so get ready to figure out the odds of your model actually making a correct guess. 🎲

