
I like to consider Linear Algebra the “Wi-Fi” of machine learning. It’s invisible, but nothing works without it.
Today, let’s zoom in on five of the biggest hitters in ML that lean on linear algebra like managers lean on meetings that could’ve been emails.

📈 Linear Regression - Ultimate “Line of Best Fit”
What It Is:
At its heart, Linear Regression is about finding a straight line (or a flat plane in higher dimensions) that best describes the relationship between your input data and the output you're trying to predict.
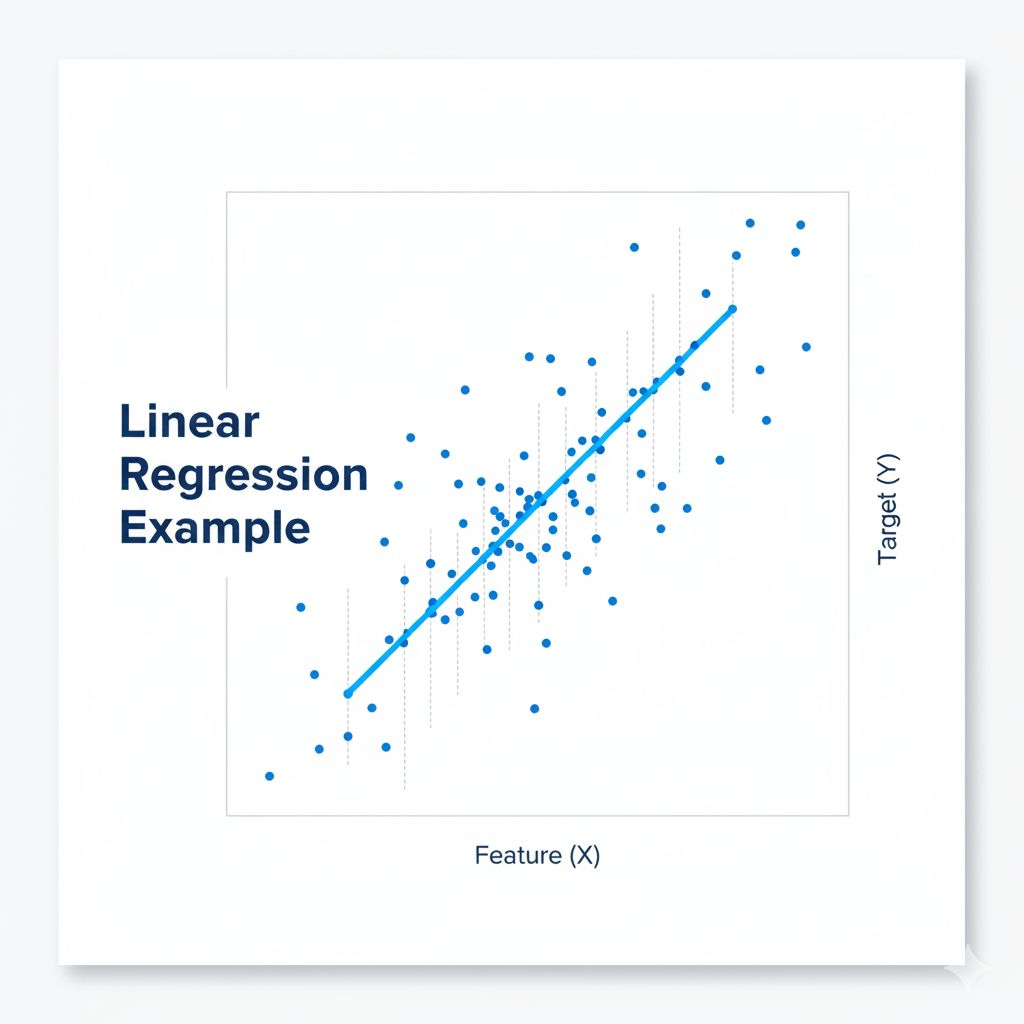
How Linear Algebra Plays A Role:
Imagine your dataset is a giant spreadsheet.
Your entire data (all the feature columns, like 'size,' 'age,' etc.) is put into one big grid of numbers called the Data Matrix (X).
The single column you want to predict (like 'price') is the Target Vector (y).
The algorithm needs a recipe (a vector of coefficients, β^) to combine your data columns to get close to the correct answers (y).
Linear Algebra finds the absolute best recipe (β^) that minimizes the prediction error.
The perfect "recipe" vector (β^) is found using the Normal Equation: β^=(XTX)−1XTy
Basically, linear algebra solves linear regression by treating the dataset like a matrix equation. In other words, it forces your scattered data to behave.


🔍 Principal Component Analysis (PCA) - “Data Simplifier”
What It Is:
Ever had a dataset with hundreds or thousands of features, making it slow to process?
Principal Component Analysis (PCA) is a technique that reduces high-dimensional data into fewer dimensions. Basically, it’s your data on a diet—same flavor, fewer carbs.
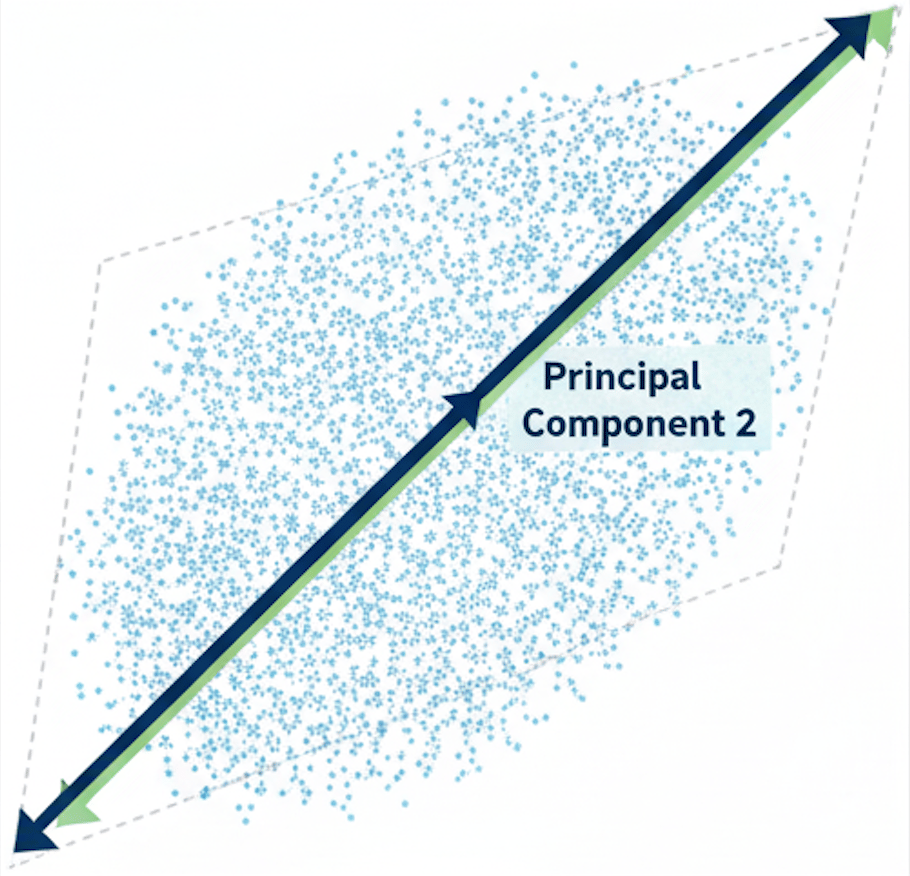
How Linear Algebra Plays A Role:
Think of someone you know who is a master selfie-taker. They seem to know the right angle, lighting, and face expressions to create the ultimate catfish for their next date.

PCA does the same thing with data (minus the catfish part).
Using linear algebra (eigenvectors and eigenvalues), it rotates your data to find its best angle—the one that shows off the most important patterns while hiding the irrelevant stuff.

💪 Support Vector Machines (SVM) - “Border Patrol”
What Is It:
Support Vector Machines (SVMs) are algorithms that try to draw the best possible line (or hyperplane, in higher dimensions) to separate your data into different classes.
Picture a super territorial roommate, drawing a line in the middle of a room, declaring, “This is my side, and this is your side”. That’s basically SVMs.
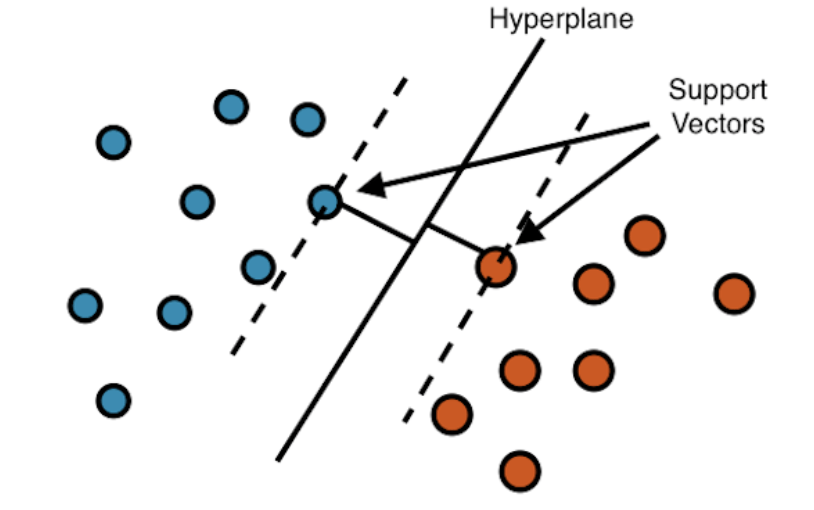
How Linear Algebra Plays A Role:
Linear Algebra shows up here in full force. The hyperplane itself is defined by a vector. Classification is achieved by calculating the Dot Product to determine which side of the plane a data point falls on.
Furthermore, there is something called the Kernel Trick for data that’s non-linear. This is where the math seems almost like sorcery!
The Kernel Trick is a powerful Linear Algebra trick that allows the algorithm to map the data to a higher-dimensional space, where linear separation becomes possible.

🪄 Singular Value Decomposition (SVD)
What It Is:
Singular Value Decomposition (SVD) is like taking a giant, messy matrix and breaking it down into three cleaner, easier-to-handle pieces. It’s a powerful technique in linear algebra that breaks down any matrix.
Think of it as providing the ultimate X-ray of your data matrix.
How Linear Algebra Plays A Role:
Given any matrix A, SVD decomposes it into the following equation:
A=UΣVT
A is your original big, complicated data matrix.
U and V are orthogonal matrices (think: nicely rotated coordinate systems).
Σ (Sigma) is a diagonal matrix with the singular values — basically, the “importance scores” that tell you which directions in your data matter most.

🧠 Neural Networks
What It Is:
A Neural Network is an algorithm designed to recognize patterns and make decisions in complex data. It's built from interconnected layers of nodes (neurons), much like the human brain.
Input Layer: Receives the raw data (e.g., pixel values of an image).
Hidden Layers: Perform the bulk of the computation, transforming the data through many stages.
Output Layer: Produces the final result (e.g., the prediction "Cat" or "Dog").
If you want to learn more about neural networks (which I highly recommend), I just did a post about it here.
How Linear Algebra Plays A Role:
Without linear algebra, you wouldn’t be able to represent the data to your neural network. Every step through the network — from input to output — is powered by matrix multiplication (an important aspect in linear algebra).
On top of this, the process of learning (adjusting weights and biases) involves gradients, which rely on matrix calculus — an extension of linear algebra.
Basically, if you have no linear algebra? No neural network, my friend.

⭐ Conclusion
Clearly, Linear Algebra isn’t just a prerequisite; it’s the secret sauce that powers the most impactful machine learning algorithms.
Nothing works without it.
And speaking of Linear Algebra…next week I’ve got something special lined up for you. While I don’t want to give away the surprise now, I’ll say this:
If any of the terms I used today—from “eigenvectors” to “Dot Product” left you scratching your head…don't worry. I've got you covered.
Catch you on the next epoch! 😉

